Elektrotechnik und Angewandte Mathematik
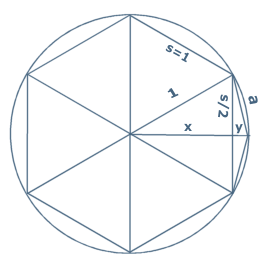
Das rechnerische Verfahren zur Ermittlung von π:
- Es gilt nach Pythagoras: s2=x2+(s/2)2
⇒ Für das Sechseck ist x=√(3/4)=0.86602 - Es gilt: y=1-x
⇒ In unserem Fall ist y=0.13398 - Wiederum nach Pythagoras: a2=y2+(s/2)2
⇒ Beim Sechseck also a=√0.26795=0.51764
⇒ π=6a=3.1058
Die Berechnung der Kreiszahl π (Pi)
Aus der Seite http://www.anderegg-web.ch
Archimedes berechnete π, indem er versuchte, den Kreis quadratisch zu machen. Dazu malte er in und um einen Kreis Vielecke mit 6, 12, 34, 48 und 96 Seiten. Der Umfang der Vielecke, die im Kreis lagen, wurde immer größer. Der Umfang der Vielecke, die um den Kreis gezeichnet waren, wurde immer kleiner. So konnte er den Wert von π eingrenzen und fand heraus, dass π größer als 3,1408 und kleiner als 3,14285 sein musste.
Tabelle der ermittelten Näherungswerte für π ("Pi"):
| n-Eck | s | x | a | a*n=π |
|---|---|---|---|---|
| 6 | 1.0000000 | 0.8660254 | 0.5176380 | 3.1058285 |
| 12 | 0.5176380 | 0.9659258 | 0.2610523 | 3.1326286 |
| 24 | 0.2610523 | 0.9914448 | 0.1308062 | 3.1393502 |
| 48 | 0.1308062 | 0.9978589 | 0.0654381 | 3.1410319 |
| 96 | 0.0654381 | 0.9994645 | 0.0327234 | 3.1414525 |
| 192 | 0.0327234 | 0.9998664 | 0.0163622 | 3.1415576 |
| 384 | 0.0163622 | 0.9999665 | 0.0081812 | 3.1415839 |
| 768 | 0.0081812 | 0.9999916 | 0.0040906 | 3.1415905 |
| 1536 | 0.0040906 | 0.9999979 | 0.0020453 | 3.1415921 |
| 3072 | 0.0020453 | 0.9999994 | 0.0010225 | 3.1415925 |
| 6144 | 0.0010226 | 0.9999998 | 0.0005113 | 3.1415926 |