Erzeugung und Größen

Grundsatz

In einer drehenden Maschine wird eine sinusförmige Wechselspannung erzeugt.

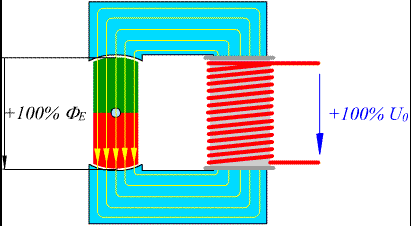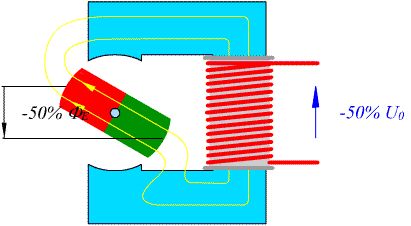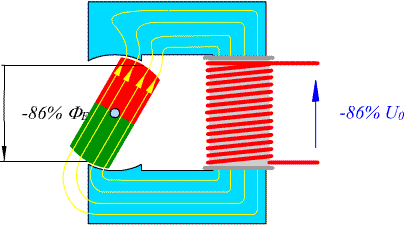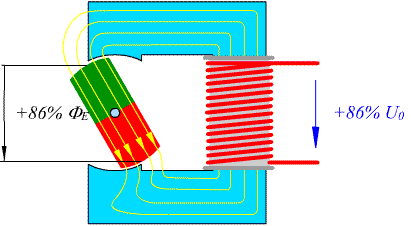
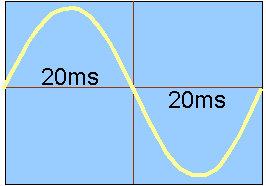
Die Ausgangsspannung eines Wechselstromgenerators wird mit Hilfe eines Oszilloskops gemessen. Das Messergebnis zeigt eine sinusförmige Schwingung oder eine Wechselspannung.

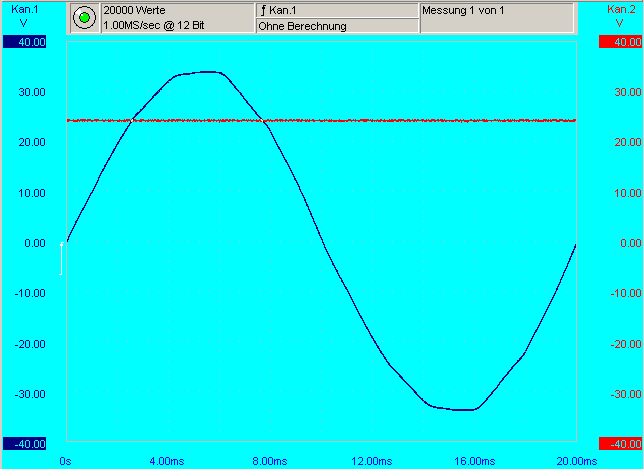
Periodendauer und Frequenz

Ein Zahlenbeispiel:

Im Beispiel ist T = 40ms. Um herauszufinden, wieviele Perioden die Spannung in einer Sekunde hat, setzen wir den folgenden Schluss an: 40 ms ................................ 1 Periode 1000 ms ................................ ? ______________________________________________________

Das Zahlenbeispiel zeigt uns, dass man die Frequenz aus dem Kehrwert der Periodendauer in Sekunden erhält:

Die Frequenz der Wechselspannung entspricht der Drehzahl des Magneten.

Die Frequenz f und die Periodendauer T berechnet man jeweils aus dem Kehrwert des Anderen:

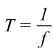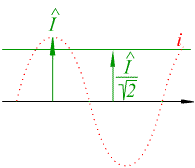
Spitzen- und Effektivwert

Beide Größen hängen wieder zusammen:

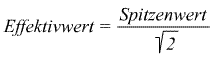Die Höhe der Schwingung ( = Amplitude) ist der Spitzenwert:

1. Spitzenwert der Spannung („U-Spitze“)
2. Spitzenwert der Induktion („B-Spitze“)

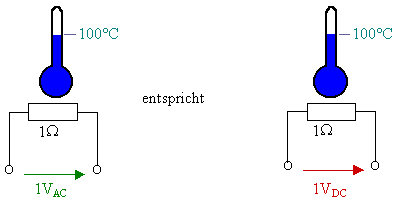
Eine Wechselspannung mit 24V_eff erzeugt an einem ohmschen Widerstand (Heizung, Lampe..) die selbe Wärme, wie eine Gleichspannung von 24V.

Der ohmsche Widerstand wird daher als Wirkwiderstand bezeichnet.

Das Feld, in das du klickst wird neu berechnet:

Geschwindigkeit bei drehender Bewegung

Allgemein gilt für die Geschwindigkeit:

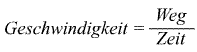
Wenn sich ein Punkt (etwa der Norpol eines Magneten) auf einer Kreisbahn bewegt, ist sein Weg der
Kreisumfang (U = 2 ^.π ^. r) und die Umfangsgeschwindigkeit v_U = 2 ^.π ^. r/t.

Die Winkelgeschwindigkeit

Wenn man sich bei der Umfangsgeschwindigkeit den Radius r = 1 denkt
und sich fragt, wie oft sich der Magnet in einer Sekunde (t = 1s) dreht (Drehzahl n),
ist das rechnerische Ergebnis die
Winkelgeschwindigkeit ω (sprich "omega") = 2 ^.π ^. Umdrehungen / Sekunde

Die Kreisfrequenz ω

Eine Umdrehung des Magneten entspricht einer Periode der Schwingung. So kann man für n = Umdrehungen / Sekunde auch f = Schwingungen / Sekunde schreiben. So entsteht die Bezeichnung Kreisfrequenz: