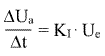Begriffe

Wie in allen Berufssfeldern gibt es auch in der Regelungstechnik eine Reihe spezieller Begriffe, die wir kennen lernen sollten. Damit läßt sich vieles einfacher erklären. auf den folgenden Seiten wird nun also versucht, verwendete Begriffe zu erklären.

Das Gemeinsame mit der Steuerungstechnik

In einen Technischen Prozess Transport von: Energie
Material oder
Information. kann durch Stellglieder über

1. eine Steuerung oder
2. eine Regelung

eingegriffen werden. Dementsprechend wird der Material-, Energie- oder Informationsfluss gesteuert oder geregelt.

Was unterscheidet das Steuern vom Regeln?

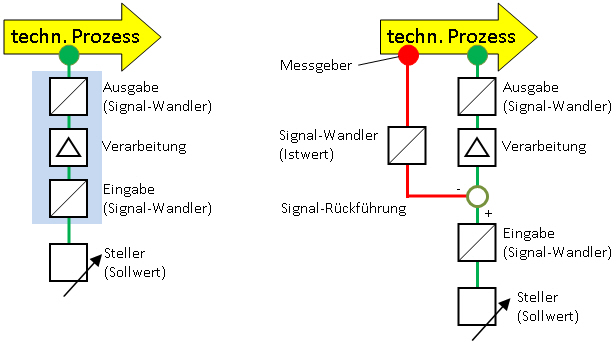
Die Signalkette beim Steuern	Der Signalkreislauf beim Regeln
Eine Änderung des Prozesszustandes hat keinen Einfluss auf die Steuereinrichtung. Ein Änderungszustand ist stabil. Wenn sich die Umgebungsbedingungen wieder ändern, müssen die Eingangsgrößen neuerlich verstellt werden, um den Prozess wieder anzupassen. Eine Steuerung ist durch den offenen Wirkungskreis ( = die Signal- oder Steuerkette) gekennzeichnet.	Der Prozesszustand wird laufend mit geeigneten Messmitteln überwacht Jede Änderung wird zum Eingang der Regeleinrichtung zurückgeführt, so dass die Signalverarbeitung laufend damit beschäftigt ist, Änderungen auszugleichen (auszregeln). Der Zustand ist daher unstabil. Eine Regelung ist durch den geschlossenen Wirkungskreis ( = den Regelkreis) gekennzeichnet.
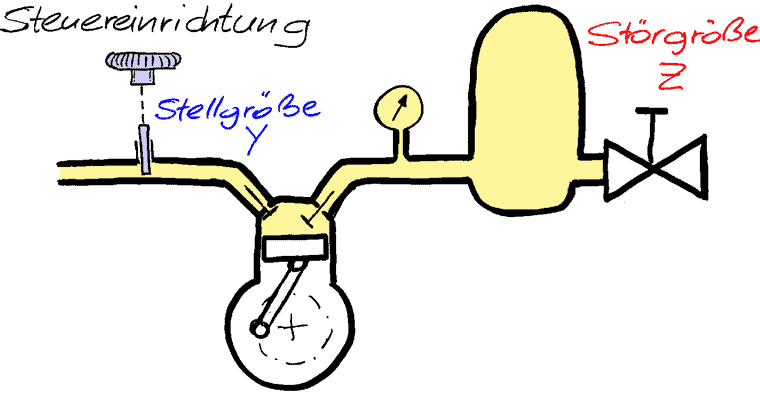
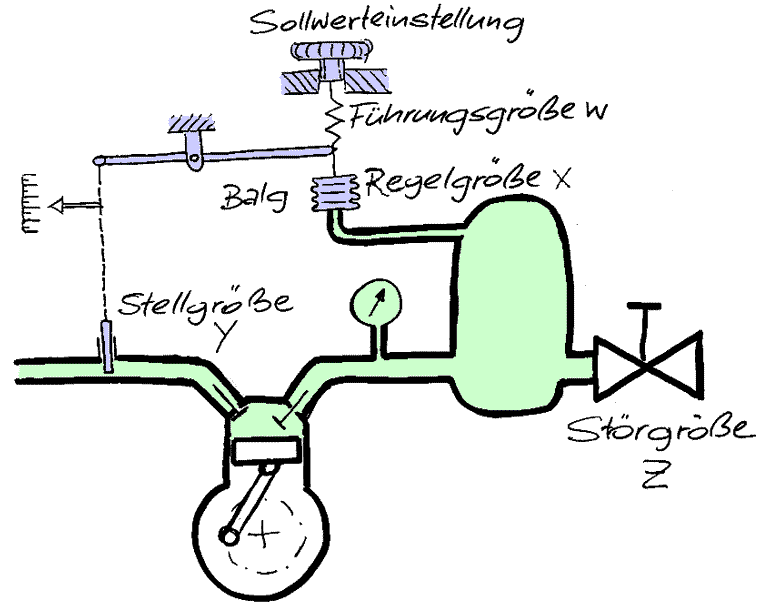
Beispiel Druckluftsteuerung	Beispiel Druckluftregelung

Schematische Darstellung einer Regelung

Dazu verwenden wir folgende Begriffe:

Auch in dieser Darstellung kommt der Geschlossene Wirkungskreis deutlich zum Vorschein.

Die Regelstrecke

In einer Regelstrecke soll eine Regelgröße „x“ durch automatische Einstellung einer Stellgröße „y“ konstant gehalten werden. Das kann nur in bestimmten, technisch realisierbaren Bereichen geschehen. Diese Bereiche nennen wir:

1. Stellbereich Y_h (Drehzahlbereich)
2. Regelbereich X_h (Spannungsbereich)

Nehmen wir doch den praktischen Fall einer Spannungsregelung eines Generators. Wir können annehmen, dass auf die Veränderung der Drehzahl eine sofortige Veränderung der Spannung erfolgt. Das Schema der Regelstrecke würde wie folgt beschriftet:

Zeitverhalten von Regelstrecken

Die unverzögerte Strecke

Bei einer solchen Strecke spricht man von einer P-Strecke.

Eine sprungartige Änderung der Stellgröße um den Wert Δy führt zu ...

... einer sprungartigen Änderung der Regelgröße um den Wert Δx.

Aus dieser Sprungantwort ergibt sich die Streckenverstärkung oder, der sogenannte Übertragungsbeiwert K_s der Strecke mit

.

Angenommen, unser Antrieb des Generatorsatzes ändert die Drehzahl von 2500U/min auf 2600U/min, damit würde sich die Ausgangsspannung von 230V auf 241V erhöhen. Dann kann der Übertragungsbeiwert KS in folgenden Zahlen ausgedrückt werden. Das Ergebnis bedeutet nichts Anderes, als dass bei der Ab- oder Zunahme der Drehzahl sich die Generatorspannung um 0,11V je Umdrehung ändert.

Strecke mit Verzögerung

Die meisten Regelaufgaben umfassen Strecken mit Verzögerungen. Diese Strecken besitzen einen sogenannten Ausgleich. Das bedeutet, dass die Regelgröße nach einer bestimmten Zeit den sogenannten Beharrungszustand erreicht hat.

Die Form, wie die Regelgröße x ansteigt, wird in der Mathematik mit dem Begriff Exponentialfunktion bezeichnet. Daher lassen sich regeltechnische Prozesse auch schön in mathematische Formeln pressen. Wir wollen uns aber auf die Wörter konzentrieren.

Die Kennzahl dieser Funktion ist die 1/5 der Zeit bis zum Erreichen des BeharrungszustandesZeitkonstante Ts.

Für unseren Generator ist das so: Wenn wir den Antrieb beschleunigen, wird sich der Maschinensatz nach und nach auch beschleunigen - je nach Größe und Trägheit des Systems - und bald mit einer schnelleren Drehzahl laufen. Das Zeitdiagramm sieht wie folgt aus:

Diese Strecke hat einen allgemeinen Namen, der sich auf ihre Verzögerung bezieht. Eine Strecke mit diesem Zeitverlauf nennt man PT₁ - Strecke, oder Strecke Erster Ordnung.

PT₁ - Strecken erreichen nach einer vorgegebenen Funktion ihre Momentanwerte und nach fünf Zeitkonstanten den Beharrungszustand.

Jetzt können wir unser Generatorbeispiel ergänzen. Die Strecke kann in zwei Glieder zerlegt werden, wovon der Generator schon berechnet wurde und der Antriebsmotor bei Volllast 12 Liter Brennstoff je Stunde verbrennt. Daraus läßt sich auch der StreckenverstärkungÜbertragungsbeiwert für den Antrieb des Generators berechnen. Für die gesamte Strecke sieht das Schema dann so aus:

Strecken höherer Ordnung

PT₁ - Strecken enthalten ein Verzögerungsglied in der Strecke.

PT_x - Strecken enthalten mehrere Verzögerungsglieder hintereinander

Das Zeitverhalten solcher Strecken wird zusehends ungünstiger für den Regelfall. Wie soll sich ein Regler verhalten, wenn trotz Anstieg der Stellgröße y des Reglers sich die Regelgröße x zuerst gar nicht ändert dann jedoch plötzlich sehr schnell. Im Diagramm zum Zeitverhalten ist im Verlauf deutlich ein Wendepunkt zu sehen. Am Start zeigt die kleine Steigung der Kurve den zunächst zähen Anstieg der Regelgröße an.

Für die Regelbarkeit einer Strecke ist das Verhältnis von Ausgleichszeit T_g und Verzugszeit T_U maßgebend. Als Grenze gilt der Wert "2".

Den Extremfall für verzögerte Strecken bilden Förderbänder, bei denen es zu sogenannten T_g ist einige Sekunden und T_U ist praktisch "0"Totzeiten kommt. Diese lassen sich so einfach nicht mehr regeln. Die Sprungantwort sieht dann so aus.

Reglergrundlagen

Aufgabe eines Reglers ist es, die Abweichung einer Istwert der Regelgröße X_RGröße von ihrem eingestellten der Führungsgröße WWert automatisch auzugleichen. Der Unterschied zweier Größen ist nichts Anderes als die rechnerische Differenz zweier Zahlenwerte. Womit wir wieder in der Mathematik gelandet sind.

Ein wesentlicher Baustein eines Reglers ist der Vergleicher (s.o.). Hier wird diese Differenz gebildet. Daraus erklärt sich auch die Vorzeichenumkehr bei der Signalrückführung aus der Regelstrecke. Eine Differenz oder der Vergleich zweier Größen ist ja nur die Summe einer positiven und negativen Zahl.

Der Großvater aller Regler

Im Schema der Drehzahlregelung einer Dampfmaschine erkennen wir schnell die wesentliche Funktion eines Proportional-Reglers. Wenn die Maschinendrehzahl steigt, hebt sich das Fliehkraftpendel und die Steuerstange wird angehoben. Der Hebelarm a wird bewegt und im Maße der Hebelübersetzung wird der Hebelarm b dagegen bewegt. Das Dampfventil wird in dem entsprechenden Verhältnis geschlossen und die Maschinendrehzahl wird gedrosselt.

Die Hebelübersetzung ist das Verhältnis der Länge der Hebelarme. In der Regelungstechnik nennt man diese Hebelübersetzung Reglerverstärkung oder noch spezieller den Proportionalbeiwert K_P des P-Reglers.

Elektronische Regler

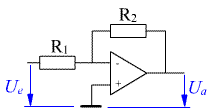
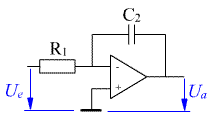
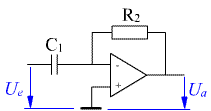
Der Operationsverstärker ist die typische elektronische Schaltung, mit der analoge Regelungsaufgaben einfach gelöst werden können. Die Schaltung für den P-Regler sieht folgendermaßen aus:

In dieser Schaltung ist die Reglerverstärkung das Verhältnis der Widerstände. Die Größen müssen über geeignete Wandler in Spannungen umgewandelt werden. Der Stellbereich des Reglers ist durch die Versorgungsspannung der elektronischen Schaltung begrenzt. Der Regelbereich ist dementsprechend anzupassen.

Wenn man die elektronische Reglerschaltung ausmisst (siehe Labor), kann für den P-Regler folgendes Diagramm gezeichnet werden. Daraus können zwei Formeln (Verstärkung und Geradengleichung) für die Reglerfunktion geschrieben werden.

Generatorspannungsregelung

Unser Generatorsatz soll nun mit einem P-Regler ausgeregelt werden. Der Regler braucht dafür die Reglerverstärkung Das Reglerdiagramm sieht dann so aus:

Zusammenfassung aller Größen

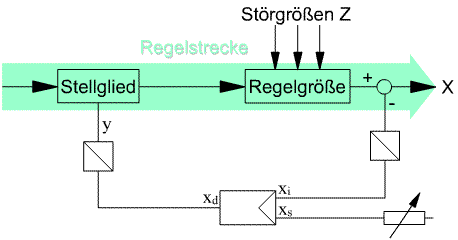
x_i ... Istwert der Regelgröße (Momentanzustand der Regelstrecke)
x_s ... Sollwert der Regelgröße (Vorgabewert aus der Führungsgröße w)
x_d ... Regeldifferenz aus dem Vergleich des Ist- und Sollwertes (x_d = x_s - x_i)

Allgemein kann die Regelung einer Regelgröße x als Vergleich ihres Istwertes x_i mit ihrem Sollwert x_s aus der Führungsgröße w betrachtet werden.

Zweck ist die Aufrechterhaltung eines bestimmten Wertes, eben auch deshalb, weil mit verschiedenen Störgrößen Z gerechnet werden muss. Sie beeinflussen die Regelstrecke von außen und verändern dabei die Regelgröße.

Die Vergleichsfunktion des Reglers mit dem internen Verstärker für die Stellgröße schafft dann den Ausgleich. Wird die Regelgröße vergrößert, verkleinert der Regler die Stellgröße (und umgekehrt). Dieser Vorgang wird durch das Vorzeichen (beachte die Vorzeichenumkehr) an der Messstelle ( = Kreis) in der Regelstrecke angedeutet.

Typen von Reglern

Grundsätzlich gibt es drei verschiedene Reglertypen, die alleine oder kombiniert verwendet werden können. Die folgende Tabelle zeigt die drei Reglertypen mit ihren wichtigsten Merkmalen:

P-Regler	I-Regler	D-Regler
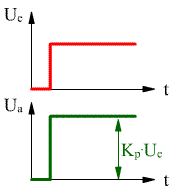
Die Sprungfunktion ( = einschalten einer Eingangsspannung) zeigt am deutlichsten den Unterschied der Reglerfunktion.
Die Reglerverstärkung wird als "Beiwert" bezeichnet:
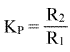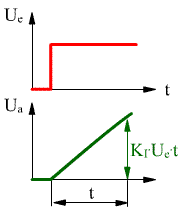
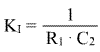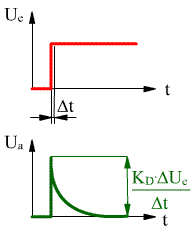
So ist der Proportionalbeiwert KP	der Integrierbeiwert KI	und der Differenzierbeiwert KD
die Ausgangsspannung des Reglers um ist um KP höher als seine Eingangsspannung	die Ausgangsspannungsänderung des Reglers ist um KI höher als seine Eingangsspannung	der Ausgangsspannungsimpuls des Reglers ist um KD größer als die Eingangsspannungsänderung

Der Reglervorgang oder "Das Regeln"

Regler haben die Aufgabe, Regeldifferenz: x_d = x_s - x_ivom Sollwert abweichende Signale so schnell wie möglich auszugleichen.

Wie antwortet ein Regler?

Grund für eine Abweichung ist im geschlossenen Regelkreis immer eine Störgröße.

Der Proportional- oder P-Regler reagiert auf eine Regelgrößenverkleinerung mit einem verstärkten Stellsignal:

Der Integral- oder I-Regler reagiert auf diese Regelgrößenverkleinerung mit einem stetig anwachsenden Stellsignal:

Der Differential- oder D-Regler reagiert auf die Regelgrößenverkleinerung mit einem kurzen positiven Stellimpuls:

Reglersymbole und Kenngrößen

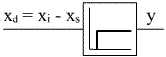
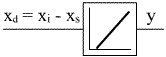
Die Symbolik der Regler lehnt sich an die Sprungantwort an:
P-Regler	I-Regler	D-Regler
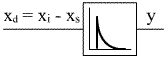Es müssen ja nicht unbedingt nur Spannungen geregelt werden. Die Funktion der Regler ist allgemein gesagt die Reaktion des Reglers auf die eingehende Regeldifferenz xd mit der Verstellung der Stellgröße y.
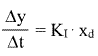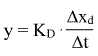Die Verstellung der Stellgröße y ist proportional der Regeldifferenz xd. Gibt es keine Regeldifferenz, gibt es auch kein Stellsignal. Der P-Regler braucht immer eine Regelabweichung!	Die Stellgrößenänderung Δy / Δt ist proportional der Regeldifferenz xd. Der Regler führt bei einer Regeldifferenz bis zur Grenze des sogenannten Stellbereiches. Dies umso schneller, je größer die Regeldifferenz ist.	Die Verstellung der Stellgröße y ist proportional der Regelgrößenänderung Δxd / Δt. Wenn sich die Regelgröße zeitlich ändert, reagiert der Regler schnell mit einem impulsförmigen Stellsignal.

Regelungstechnik Zusammenfassung