 Lehrstoffverteilungen für
Fachkunde |
Elektrotechnik |
Fachzeichnen |
Laborübungen
Lehrstoffverteilungen für
Fachkunde |
Elektrotechnik |
Fachzeichnen |
Laborübungen Fragen
FragenSRT-Digitaltechnik (Grundlagen)
[FK/EMT]
Die Signalisierung von Information
Für eine Maschine ist es nicht so einfach, verschiedene Signale zu empfangen, und sie dann zuverlässig unterscheiden sowie verarbeiten zu können. Damit ist das Problem kurz umrissen.
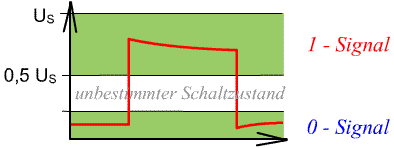 Signalhub (rote Linie) zwischen den Zuständen: "logisch 0" und "logisch 1". |
In der Digitaltechnik werden Informationen in Form von elektrischen Signalen verarbeitet. Der Einfachheit halber konzentrieren wir uns auf die Signalspannung |
Wie mehr als zwei Information in einer binären Form ( = aus zwei Einheiten bestehend) verarbeitet werden können, zeigt der folgende Absatz.
Codierung von Information
1. Das Dezimalsystem
Ausgangspunkt sind die Zahlensysteme. Wir verarbeiten gewöhnlich Informationen im Dezimalsystem. Das bedeutet unsere Zahlen setzen sich aus 10 möglichen Werten (0...9) und Stellen mit Zehnerpotenzen zusammen. Nehmen wir die Zahl 247 als Beispiel, kann sie folgendermaßen erklärt werden:
| Stelle | Wertigkeit | Zehnerpotenz | ergibt |
|---|---|---|---|
| Hunderter | 2 | . 102 = | 200 |
| Zehner | 4 | . 101 = | 40 |
| Einer | 7 | . 100 = | 7 |
| _______________________________________________________ | |||
| Das ergibt die Summe von 247 | |||
Die Hauptrolle neben den Zahlenzeichen spielen die Stellen, also die
Das Dualsystem
Maschinen arbeiten mit Informationen im
| bit | Wertigkeit | Zehnerpotenz | ergibt |
|---|---|---|---|
| 64-er | 1 | . 26 = | 64 |
| 32-er | 0 | . 25 = | 0 |
| 16-er | 1 | . 24 = | 16 |
| 8-er | 1 | . 23 = | 8 |
| 4-er | 0 | . 22 = | 0 |
| 2-er | 0 | . 21 = | 0 |
| 1-er | 1 | . 20 = | 1 |
| _______________________________________________________ | |||
| Das ergibt die Summe von dezimal 89 | |||
Die für uns gängige Zahl "89" muss in einer Maschine durch sieben einzelne Datenleitungen dargestellt werden. Jede Leitung stellt dabei ein
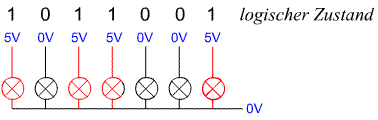
Dieses Muster, also die bit-Folge
Logische Operationen
Maschinen können mit Dualzahlen rechnen. Dazu benötigt man Schaltungen, die wir bereits in den Relaisschaltungen kennengelernt haben. Alle Schaltungen folgen den Gesetzen des elektrischen Stromkreises. In der Digitaltechnik wird die Symbolik ( = Darstellungweise) weiter vereinfacht.
Und - Funktion
Die Schaltung liefert eine Ausgangsspannung (für eine Relaisspule ...), wenn der Schalter S1
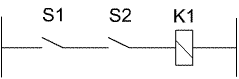 |
||||||||||||||||||||
| Der Kontaktplan (KOP) zeigt den Strompfad der angesteuerten Relaisspule: | Der Funktionsplan (FUP) ist eigentlich rein symbolisch, allerdings gibt es tatsächlich Bauelemente, die diese Funktion beherrschen: | Die Boole'sche Algebra ist bewußt an die mathematische Schreibweise angenähert. Es gibt in der Logik ebenfalls "Vorrangregeln". So entspricht der bekannten Rechenregel: Punkt vor Strich die Regel Und vor Oder: |
||||||||||||||||||
| Die Darstellung der Wahrheitstabelle zeigt den logischen Signalzustand des Ausgangs (letzte Spalte) in Folge der Eingangszustände (ersten zwei Spalten): |
|
|||||||||||||||||||
Oder - Funktion
Die Schaltung liefert jetzt eine Ausgangsspannung, wenn der Schalter S1 oder wenn der Schalter S2 geschlossen wird.
| KOP: | FUP: | Boole'sche Algebra: | ||||||||||||||||||
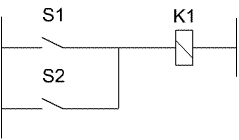 |
||||||||||||||||||||
|
||||||||||||||||||||
Umkehr - Funktion
Die Schaltung liefert dann eine Ausgangsspannung, wenn der Schalter S1
| KOP: | FUP: | Boole'sche Algebra: | |||||||||
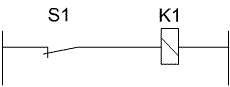 |
|||||||||||
|
|||||||||||
Die klassiche Wechselschaltung als logisches Problem
Die Wechselschaltung besteht in der Sprache der Steuerungstechniker aus zwei Umschaltern ( = Wechselschalter) in Serie. Der Stromlaufplan führt die Funktion (hoffentlich) deutlich vor Augen:
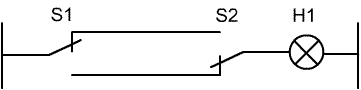
Die Logik kennt nur öffner- und Schließer-Kontakte, die den Wechselschalter aber problemlos ersetzen können:
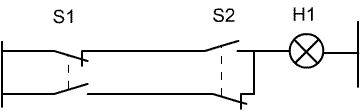
Nun kann nach allen "Regeln der Kunst" ( = Digitaltechnik) der Funktionsplan die boole'sche Algebra und die Wahrheitstabelle aufgestellt werden:
| FUP: | Boole'sche Algebra: | |||||||||||||||||||
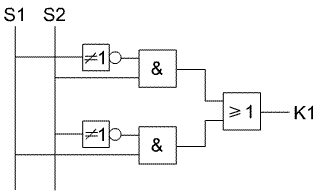 |
Der Ausgang wird über zwei Bedingungen geschaltet:
Sie können mit einem logischen OR zusammengefasst werden: |
|
||||||||||||||||||
Die Wahrheitstabelle liefert ein interessantes Ergebnis. Der Ausgang führt dann eine Spannung, wenn sich die beiden Eingänge S1 und S2 unterscheiden. Ihr Status ( = Wert) entspricht sich nicht, deshalb spricht man von einer Antivalenz. Klingt doch gut, oder? Die Sache ist die: Für diese Funktion gibt es in der Digitaltechnik ein eigenes Symbol. Die Verknüpfung ( = Operation) heißt
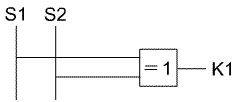
Von der Kreuzschaltung zum BCD-Code
Wie unterscheidet sich die Kreuzschaltung von der Wechselschaltung oben? Es kommen beliebig viele Schalter dazu, wobei jeder die Möglichkeit der Auschaltung (oder Einschaltung) der Lampe H1 erhöht. Aber wie? Sehen wir doch die Schalter als bit einer Dualzahl (siehe Funktionsplan oben). Damit ergeben sich für drei Schaltstellen 20 + 21 + 22 gleich 8 Möglichkeiten (mit Null), die Lampe abwechselnd ein- und auszuschalten. Stellen wir die Wahrheitstabelle (rechts) so zusammen, dass sich immer ein bit ändert (das entspricht immer einem Schaltschritt), dann wird genau das abwechselnde Ein- und Ausschalten abgebildet: |
| ||||||||||||||||||||||||||||||||||||||||
Für alle Zeilen in der Wahrheitstabelle, in denen H1 = 1 gilt, was jene Schalterstellung ist, bei der die Lampe leuchtet, ergibt sich der folgende boole'sche Ausdruck:
![]()
Die übersicht in der obigen Tabelle ist allerdings nicht gerade groß. Besser wäre es, dual richtig zu zählen und dann alle Möglichkeiten für den Ausgang zu prüfen. Die folgende Tabelle zeigt die richtige duale Zählweise anhand eines wichtigen Codes.
Der BCD - Code
Der Binary Coded Decimal - Code arbeitet mit 4 bit und ist ein Musterbeispiel der dualen Ordnung. Die vier Bits (8 - 4 - 2 - 1) werden als Half-Byte bezeichnet. Demnach besitzt ein Byte also acht Bit Breite. Mit vier Bits können insgesamt 16 Informationen ( = Hexadezimal- kurz HEX-Code) codiert werden. Jedes weitere Bit verdoppelt den Informationsgehalt (1 - 2 - 4 - 8 - 16 - 32 - 64 - 128 - 256 ... sind alles Zweierpotenzen!). |
|